为何蜜蜂会打造出完美的六边形蜂巢？

自然界中有不少神奇现象令人震撼，你能想到蜂巢、肥皂泡和海绵外骨骼之间的奇妙联系吗？答案是它们钟爱六边形。为何蜜蜂会打造出完美的六边形蜂巢？这当然不是什么神秘的力量，而是其中富含的深刻数学和物理学道理。

撰文 ｜ Philip Ball

编译 ｜ 顾淼飞

蜜蜂，天生的数学家？

蜂巢简直是个工程学奇迹：它由一排排棱镜似的“小隔间”组成，每一个“小隔间”的横截面都是完美的六边形；由蜂蜡制成的墙壁，每一面的厚度都相当精确；所有的房间沿水平方向微微倾斜，不仅避免蜂蜜从蜂巢里流出来，还让整个蜂巢的方向与地球磁场方向一致。

蜜蜂在动工之前并没有做过统筹规划，也不可能拿到设计图纸，它们却能分工合作，鬼使神差地完成了如此精妙绝伦的蜂巢。

蜜蜂是怎么做到的？

古希腊哲学家帕普斯（Pappus of Alexandria）认为，蜜蜂一定天赋异禀，有着“几何学的远见卓识”。那么，又是谁给了它们这种远见卓识，似乎只能是上帝吧？莫非蜜蜂果真像威廉·柯比（William Kirby）在1852年说的那样，是“天生的数学家”？不管你信不信，反正达尔文不信。达尔文认为主导这一切的是进化论，而不是什么神祗的力量，于是他进行了一系列实验，想证实蜜蜂是否仅凭进化和遗传得来的本能就可以建造出完美的蜂巢。

下一个问题是，为什么是六边形？这其实是一个很简单的几何问题。假设我们想用相同形状和大小的图形密铺一个平面（使图形不留空隙、也不互相重叠地铺满整个平面），那么只有3种正多边形可以做到：正三角形、正方形和正六边形。（这里指规则镶嵌。关于不规则镶嵌可参见《彭罗斯：不思考生物化学的诺贝尔物理学奖得主不是好的数学家》。）在铺满同等面积的情况下，使用正六边形所需要的周长之和最小。这就不难理解蜜蜂为什么会选择六边形了，因为蜂巢是用蜂蜡做的，而蜜蜂产出蜂蜡是消耗能量的，它们当然希望省些力气——这点小心思就跟打工人想少搬几块砖一样。

人们早在18世纪就明白了这一点，用达尔文的话说，六边形的蜂巢是“最省劳动力、也最省材料的选择”。他认为，既然六边形蜂巢所需要的能量和时间是最少的，那么在自然选择的作用下，这种建造方式就成了蜜蜂的本能。不过，就算蜜蜂真的会测量巢房的角度，会测量墙壁的厚度，它们也未必需要依赖这种本能。因为，创造六边形是大自然一贯的做法。

大自然更爱“斤斤计较”

如果你在水面上吹一层泡泡——也就是“泡泡筏（Bubble raft）”——这些泡泡最后都会变成六边形或者近似于六边形的形状。你不可能看到有哪个泡泡筏里全是正方形的泡泡，如果有4个泡泡聚集在了一起，它们会马上重新排列成“三足鼎立”的样子，交界处就像经典的奔驰标志，三边相接，夹角差不多都是120°。

单层的“泡泡筏”由大多数六边形（不一定是正六边形）的泡泡组成。有一些“缺陷”泡泡可能有五面或七面。但三边相交，角度约为120°。图源：Shebeko ／ Shutterstock

蜂巢中的六边形尚且有个“幕后推手”——说的就是蜜蜂，而泡泡筏中的六边形可并没有什么神秘力量在驱使。如果硬要说有，那么这个神秘力量就是物理学规则。（参见《数理史上的绝妙证明：简单泡泡背后的恐怖数学》）

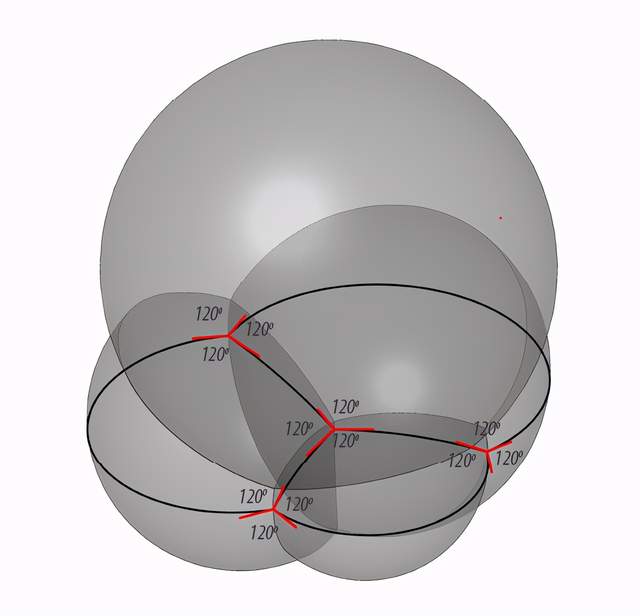
如果我们从平面的泡泡筏推演到立体的“泡泡堆”，结果也是类似的。假如你用吸管对着一碗肥皂水吹气，吹起一堆泡沫，你会看到，当泡泡堆积在一起之后，它们四面边界相交于一个点，夹角约为109°——没错，这个角度就是正四面体中心到各顶点连线的夹角。