国务院关于印发《2024—2025年节能降碳行动方案》的通知
首页 >
BMS未准确定义 SOC何来高精度（二）
来源：
时间：2018-09-04 23:57:56
热度：
BMS未准确定义 SOC何来高精度（二）在《BMS未准确定义 SOC何来高精度（一）》一文中，笔者谈到了若要准确定义SOC需要考虑容量性质维度和温度状态维度，并得到了V2.0版本的
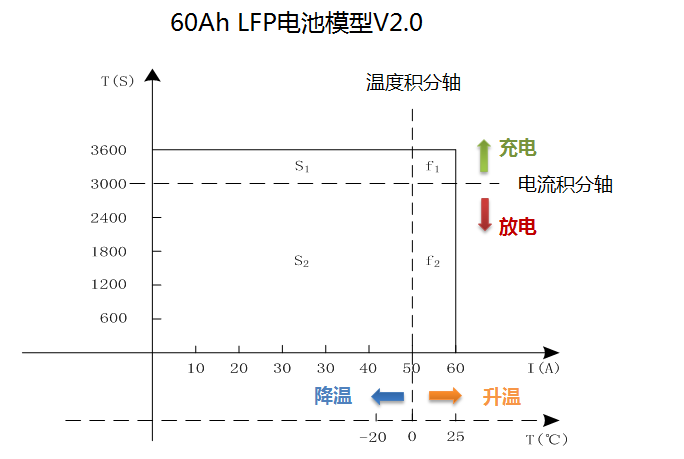
在《BMS未准确定义 SOC何来高精度（一）》一文中，笔者谈到了若要准确定义SOC需要考虑容量性质维度和温度状态维度，并得到了V2.0版本的计算模型。通过这个模型我们可以看到若以25℃的可用电量评价SOC，则SOC = (S2 + f2)/(S1 + S2 + f1 + f2)。
若以实时温度的可用电量评价SOC，则SOC = S2 / (S1 + S2 + f1 + f2) 。显然在不同的“功能需求”下我们需要选择不同的定义。本文我们再继续讨论其他需要考虑的维度。
3.电池寿命状态维度
电池在使用的过程中寿命将逐渐衰减，衰减机理主要在于正负极材料晶体的塌陷和电极的钝化导致了有效锂离子的损失。总电量也将从BOL(Beginning of Life)向EOL(End of Life)状态趋近。因此在计算SOC时需要考虑是采用BOL时刻的总容量，还是当前寿命下的实际总容量。
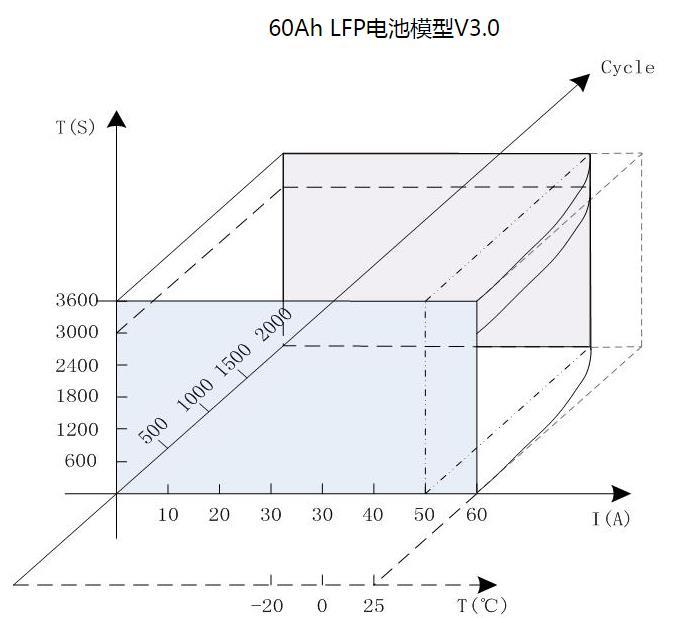
为了进一步完善算法模型可在V2.0模型的基础上增加电池循环寿命对容量的影响。将平面模型拓展成三维模型(如下图所示)，新增的Z轴坐标表示电池循环次数。该模型可以根据电池循环次数的累加，相应的减少电量模型在X、Y轴平面的投影面积，即表征电池容量随着循环次数的衰减。当然在实际应用中电池的循环次数并不能直接与总电量对应，电池电量的衰减与电池在使用过程中的充放电倍率C rate、放电深度DOD、使用温度、搁置温度等因素相关。
要解决这个问题首先需要通过电池实验找到在特定基准下的电池循环次数与电量衰减的关系。例如以70%DOD、25℃、1C倍率充放循环为基准的电量衰减特性。然后仅改变其中的单一因素进行试验(如下表所示)
DOD Factor | Temperature Factor | C Rate Factor | |||||||||||
Num | DOD（%） | T（℃） | C Rate | Num | DOD（%） | T（℃） | C Rate | Num | DOD（%） | T（℃） | C Rate | ||
1 | 50% | 25 | 1 | 1 | 70% | -20 | 1 | 1 | 70% | 25 | 0.2 | ||
2 | 60% | 25 | 1 | 2 | 70% | -10 | 1 | 2 | 70% | 25 | 0.5 | ||
3 | 70% | 25 | 1 | 3 | 70% | 0 | 1 | 3 | 70% | 25 | 1 | ||
4 | 80% | 25 | 1 | 4 | 70% | 15 | 1 | 4 | 70% | 25 | 1.5 | ||
5 | 90% | 25 | 1 | 5 | 70% | 25 | 1 | 5 | 70% | 25 | 2 | ||
6 | 100% | 25 | 1 | 6 | 70% | 40 | 1 | ||||||
7 | 70% | 55 | 1 | ||||||||||
上一篇：胶衣的使用
