首页 > 58必威网

使用信号平均来提高测量的准确性

来源：新能源汽车网

时间：2023-04-27 16:03:45

热度：

使用信号平均来提高测量的准确性我们的测量不可避免地会受到来自不同的噪声的影响。有时，我们测量的信号比噪声分量小几个数量级。在这些情况下，我们需要降噪技术以某种方式抑制噪声。在本文中

我们的测量不可避免地会受到来自不同的噪声的影响。有时，我们测量的信号比噪声分量小几个数量级。在这些情况下，我们需要降噪技术以某种方式抑制噪声。在本文中，我们将研究在特定情况下非常有效的信号平均法。

信号平均如何工作？

假设实验的输出是如图 1 所示的指数曲线。

图1

假设我们的测量设置使用 ADC 将该信号数字化。理想情况下，我们希望得到图 1 中的曲线样本；然而，实际上，噪声电压出现在 ADC 输入端并破坏了我们的样本。假设噪声分量服从均值为 0、方差为 1 的正态分布。图 2 显示了此类噪声分量的示例。

图 2

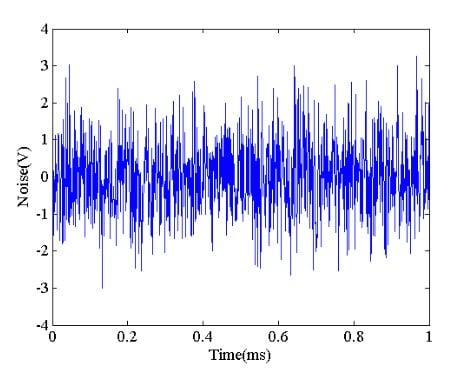
如果我们将上述噪声分量添加到图 1 所示的所需输出中，我们将获得图 3 中的波形。

图 3

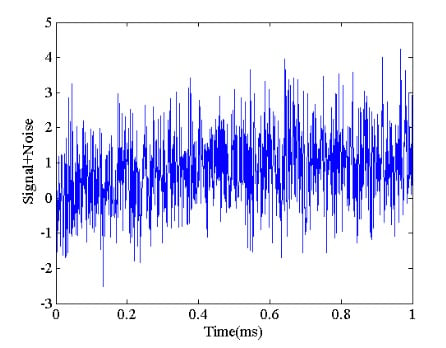
如您所见，噪声大到足以掩盖所需的输出。我们如何才能实现更准确的测量？实际上，如果某些关于噪声分量的假设是有效的，这在理论上是可能的。让我们假设噪声样本既不相互关联，也不与期望的输出相关。此外，假设噪声的平均值为零。现在，让我们重复这个实验三次，如图 4 所示。

图 4

在 t=0.3 ms 时，我们从这三个实验中得到以下值：

X 1 = S 1 + n 1 = -0.707 v

X 2 = S 2 + n 2 = 1.712 v

X 3 = S 3 + n 3 = 2.557 v

在上述等式中，当 i = 1、2、3 时，Si 表示所需的信号值，在此特定示例中为 0.7769 v（来自图 1）。然而，作为噪声分量的 n i随实验的不同而不同。由于噪声样本彼此不相关且均值为零，因此对上述三个值进行平均应该可以更好地估计所需值。我们获得：

X平均值= 1.187 v

请注意，在我们所有的实验中都相同的期望值并没有被平均过程抑制；但是，随机且均值为零的噪声分量会变小。图 5 显示了我们通过计算三个实验的平均值得到的信号。尽管平均值仍然非常嘈杂，但它的整体形状在某种程度上类似于图 1 中的指数曲线。

图 5

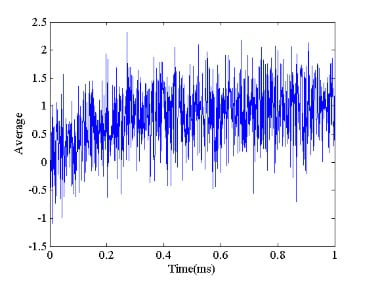
是否可以通过增加实验次数来提高准确率？图 6 显示了 100、200、300 和 400 次实验的平均输出。

图 6

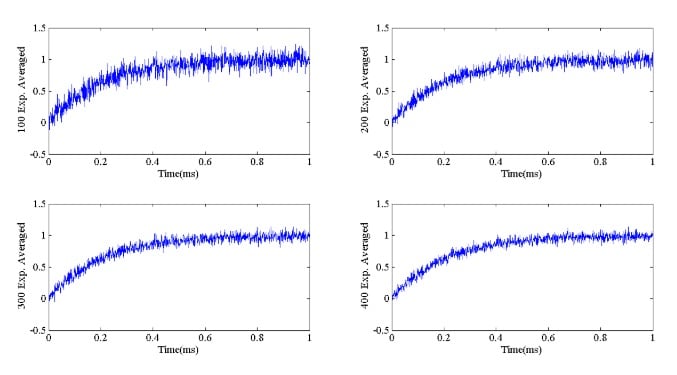
随着我们增加实验次数，我们得到越来越准确的测量结果。让我们看一下平均的数学分析，并量化增加实验次数对噪声抑制的影响。

数学分析

假设一个实验可以重复 N 次试验。如果我们用 j 表示实验编号，则第 j 个实验的输出 X j可以写为

X j = S + n j 1 ≤ j ≤ N

其中 S 表示所有这些 N 次试验都相同的期望输出，n j是影响第 j 次试验的噪声分量。与所需的输出不同，噪声分量因实验而异。假设，为了将我们的测量值数字化，我们从每个实验的输出中总共提取了 M 个样本。如果我们用 k 表示样本数，我们有

X j (k) = S(k) + n j (k) 1 ≤ k ≤ M

因此，对于给定的样本数 p，我们从这些实验中得到 N 个不同的值：

X 1 (p) = S(p) + n 1 (p)

X 2 (p) = S(p) + n 2 (p)

……

X M (p) = S (p) + n M (p)

我们看到信号平均可以抑制噪声分量。这些值的平均值是

XAvg(p)=1MM∑j=1(S(p)+nj(p)) $X_{A v g} (p) = \frac{1}{M} \sum_{j = 1}^{M} (S (p) + n_{j} (p))$

由于 S(p) 对于所有这些实验都是相同的，我们有

$X_{A v g} (p) = S (p) + \frac{1}{M} \sum_{j = 1}^{M} n_{j} (p) = S (p) + n (p)$

我们不知道影响第 j 个实验的噪声样本 n j (p) 的确切值，但我们假设它是一个均值为零且方差为 σ n 2的随机变量。为了量化信号平均对降噪的影响，我们应该计算平均噪声分量 n(p) 的方差，我们将用 σ n, avg 2表示。我们知道可以通过以下等式找到方差：

${σ_{n, a v g}}^{2} = E ([n (p)]^{2}) ? μ^{2}$

其中 E(.) 表示期望值，μ 是 n(p) 的平均值。由于假定随机变量 nj(p) 的均值为零，因此 n(p) 的均值也将为零。因此，我们有

${\sigma _{n, avg} }^2 =E\left ([n(p)]^2 \right ) =E\left [ \frac{1}{M}\sum_{j=1} ^M n_j(p)\right ]^2 = E\left ( \frac{1}{M^2}\sum_{j=1}^M n_j(p) \sum_{j=1}^M n_j( p) \右 )$

这可以改写为

${σ_{n, a v g}}^{2} = E (\frac{1}{M^{2}} \sum_{j = 1}^{M} \sum_{j = 1}^{M} n_{j} (p) n_{j} (p)) = \frac{1}{M^{2}} \sum_{j = 1}^{M} \sum_{j = 1}^{M} E (n_{j} (p) n_{j} (p))$

如果您需要查看期望运算符的属性，请观看此视频。上面的求和总共有 M 2项。其中一些涉及乘以两个不同的随机变量，即 n i (p)n j (p)，其中 i≠j。对于这些项，由于我们假设随机变量是独立的，所以我们有：

\[E(n_i(p)n_j(p))=E(n_i(p))E(n_j(p))=0 \; \; \; \; 为了 \; \; \; 我 \neq j \]

因为每个随机变量的期望值为零。然而，对于 i=j 的项，我们得到

\[E\left ( n_i(p)n_j(p) \right )=E\left ( \left [ n_i(p) \right ]^2 \right )= {\sigma_n}^2 \; \; \; \; 为了 \; \; \; 我 = j\]

总共有 M 个这样的项，因此我们得到：

${σ_{n, a v g}}^{2} = \frac{1}{M^{2}} \sum_{j = 1}^{M} \sum_{j = 1}^{M} E (n_{j} (p) n_{j} (p)) = \frac{1}{M^{2}} M {σ_{n}}^{2} = \frac{{σ_{n}}^{2}}{M}$

上面的等式表明，虽然噪声样本的方差为 σ n 2，但信号平均技术将其降低了 M 倍。请注意，所需信号不受平均的影响。因此，我们可以得出结论，信号平均可以将信噪比 (SNR) 提高 M 倍。该分析允许我们为平均技术选择所需的实验次数，以便我们可以实现任意 SNR。

通过理解以上分析，我们可以更好地了解信号平均技术的局限性。上述分析的隐含假设是：

噪声可以用零均值的随机变量建模信号和噪声不相关噪声样本彼此不相关实验可重复

信号平均依赖于噪声随机性

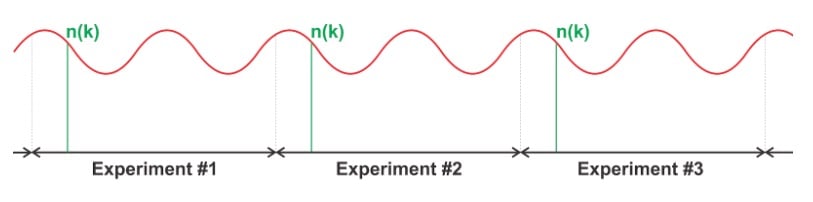
有时出现在我们测量系统输入端的噪声并不是真正随机的。例如，来自电源线的噪声会产生非随机噪声分量。假设电源线频率为 50 Hz（周期为 20 ms）并且我们每 40 ms 触发测量。如图 7 所示。在这种情况下，影响特定样本的噪声 n(k) 始终与电源线正弦波的特定部分相关。因此，平均技术不会抑制这种噪声。为了解决这个问题，我们可以简单地选择一个不能被 20 ms 整除的测量周期。或者，我们可以使用随机测量周期。